The Circle Of Thirds And Fifths

The Circle of Thirds and Fifths

You may know the circle of fifths for determining key signatures and chord relationships. I like to introduce an alternative version I call "the circle of thirds". It is formed by alternating major and minor thirds (four and three semi-tones). Combining a major third and a minor third we get a fifth, so the circle of thirds includes the circle of fifths, just go two steps at a time, or follow the points of the star!

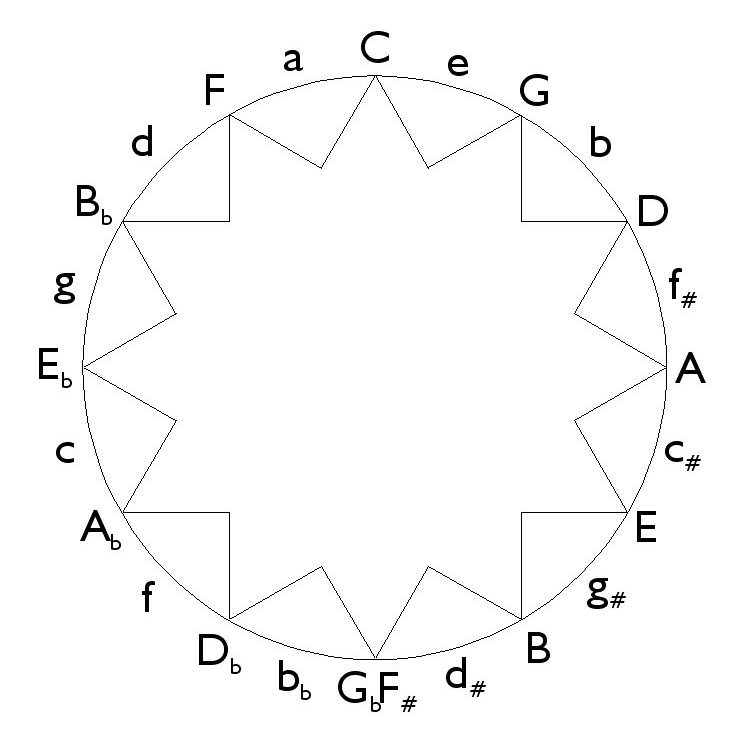
Thirds are essential for forming chords, which makes this circle of thirds so useful.

A major chord has an upper letter as its base note, then clockwise the next note is the major third and the next note of that is the fifth. And the fifth is followed by the seventh and the ninth, which are used in some chords.
For instance c-e-g are the notes of the C major chord.
A minor chord has an lower letter as its base note, then clockwise the next note is the minor third and the next note of that is the fifth, etc.
For instance a-c-e are the notes of the A minor chord.

We can see chord relationships easily as well:

For each major chord the relative minor chord starts just one step to the left (anti-clockwise).
The dominant (fifth) is two steps to the right (clockwise).
The subdominant (fourth or fifth below) two steps to the left (anti-clockwise).

So we can see the six harmonically closely related chords laid out side by side.

For example:

The G major chord notes are g-b-d
The dominant chord notes are d-f#-a
The subdominant chord notes are c-e-g
The respective relative minor chord notes are e-g-b, b-d-f# and a-c-e

These three major chords (and their three related minor chords) are built with the seven notes of the diatonic scale, and none other. On the diagram we can find the notes for a major, or natural minor, scale by using two notes left (anticlockwise) from the base note, and four notes right (clockwise) of it.

For example:

For D major look for upper case D, two left and four right give us g-b-d-f#-a-c#-e, or the notes for G major, D major and A major chords (g-b-d, d-f#-a, a-c#-e)
For D minor look for lower case d, two left and four right give us g-bb-d-f-a-c-e, or the notes for G minor, D minor and A minor chords (g-bb-d, d-f-a, a-c-e)

For other scale modes we can use different schemes:

For a Mixolydian scale look for the upper case base note, then take the next two notes clockwise and the four notes anticlockwise.
For a Phrygian scale look for the lower case base note, then likewise take the next two notes clockwise and the four notes anticlockwise.
For a Lydian scale look for the upper case base note, then take the next six notes clockwise.
For a Dorian scale look for the lower case base note, then likewise take the next six notes clockwise.

We can see that Dorian and Phrygian are different kinds of minor scales, and Lydian and Mixolydian different kinds of major scales.

Extending the basic chords:
Starting clockwise from a base note (tonic) the next note is the third, followed by the fifth, the seventh and the ninth.
For example:

Starting with upper letter C we get c-e-g-b, which is C major with 7th, or Cmaj7.
Starting with lower letter a we get a-c-e-g, which is A minor with 7th, or Amin7.

For a dominant seventh chord we need to flatten the seventh of a major seventh chord, i.e. the third note clockwise from the major (upper case) base note.
For example:

Starting with upper case G we get g-b-d-f# (G major 7), flatten the f# to f gives us g-b-d-f, or G dominant 7. Note that G is the dominant of C, and f is in the C scale, but not f#.

From adding a seventh we can extend chords further adding a ninth:
For example:

Five consecutive notes from an upper case letter gives a major 9th chord
c-e-g-b-d = Cmaj9 = C major 9th
With a flattened seventh it becomes a dominant seventh plus ninth
c-e-g-bb-d = C9
Five consecutive notes from a lower case letter gives a minor 9th chord
a-c-e-g-b = Am9 = A minor 9th

I hope this circle of thirds (and fifths) can aid you in finding chords and harmonic chord relationships!

Download pdf file for printing (114 Kb).